1. 分数坐标转笛卡尔坐标

$\begin{cases} x_i^{cart} = x_i^{frac} * x_A + y_i^{frac} * x_B + z_i^{frac} * x_C \\ y_i^{cart} = x_i^{frac} * y_A + y_i^{frac} * y_B + z_i^{frac} * y_C \\ z_i^{cart} = x_i^{frac} * z_A + y_i^{frac} * z_B + z_i^{frac} * z_C \end{cases}$

其中，$A, B, C$为POSCAR中的基失，即：

$\begin{cases} A(x_A, y_A, z_A) \\ B(x_B, y_B, z_B) \\ C(x_C, y_C, z_C) \end{cases}$

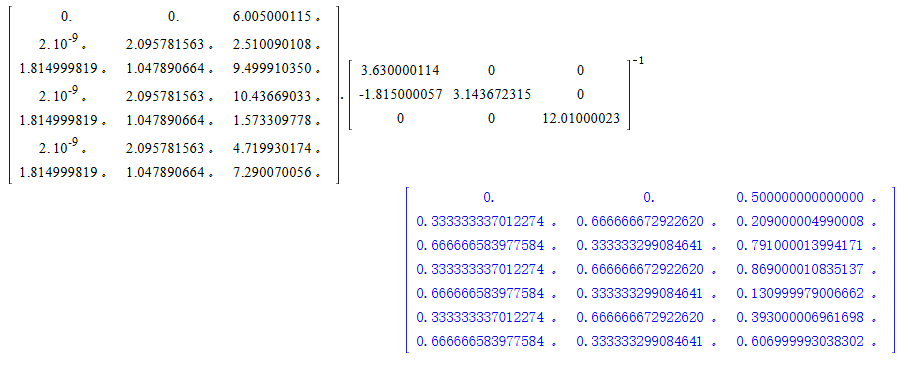
用矩阵表示为 分数坐标 × 基失 ，如下：

2. 笛卡尔坐标转分数坐标

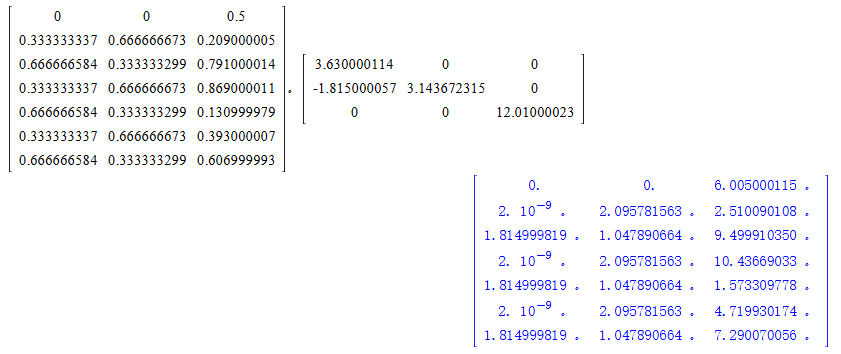
即分数坐标转笛卡尔坐标的逆过程，用矩阵表示为 笛卡尔坐标 × 基失的逆矩阵 ，如下：